Uji Hipotesis Dua Mean Populasi Beserta Contoh

 Pada uji hipotesis dua mean populasi dengan sampel yang berdistribusi normal, prosedurnya hampir identik dengan uji hipotesis satu mean. Ada tiga bentuk perumusan hipotesis yang dapat digunakan, yaitu:

1. Hipotesis nol (Ho): μ₁ = μ₂
   Hipotesis alternatif (Ha): μ₁ ≠ μ₂

2. Hipotesis nol (Ho): μ₁ ≤ μ₂
   Hipotesis alternatif (Ha): μ₁ > μ₂

3. Hipotesis nol (Ho): μ₁ ≥ μ₂
   Hipotesis alternatif (Ha): μ₁ < μ₂

Pengujian dilakukan dengan tingkat signifikansi (α) yang umumnya berada di rentang 0,01 hingga 0,05.
*) Statistik uji yang digunakan akan berbeda tergantung pada ukuran sampel

Kesimpulan:

Dengan membandingkan nilai t hitung dengan t tabel, kita dapat menentukan apakah hipotesis nol (Ho) diterima atau ditolak.

Contoh:

Seorang peneliti di sebuah pabrik lampu ingin menguji perbedaan umur rata-rata antara dua jenis bola lampu, yaitu merk "A" dan merk "B". Peneliti mengambil sampel sebanyak 150 buah bola lampu merk "A" dengan rata-rata daya tahan 887 jam dan standar deviasi 92 jam. Sementara itu, sampel dari 150 bola lampu merk "B" memiliki rata-rata daya tahan hidup 952 jam dengan standar deviasi 85 jam.

Berdasarkan data tersebut, ujilah hipotesis ini menggunakan tingkat signifikansi 0,05. Apakah ada perbedaan signifikan dalam daya tahan antara kedua merk bola lampu tersebut?

Hipotesis:

1. Hipotesis nol (Ho): μ₁ = μ₂ Hipotesis alternatif (Ha): μ₁ ≠ μ₂
2. Tingkat signifikansi (α): 0,05
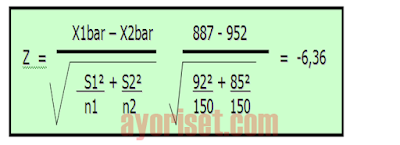
3. Statistik uji:

1. • Zα/2 = 1,96
   • Hipotesis nol ditolak apabila: Z < -Zα/2 atau Z > Zα/2

Kesimpulan:

Karena nilai Z hitung = -6,36 lebih kecil dari -Zα/2 = -1,96, maka hipotesis nol (Ho) ditolak dan hipotesis alternatif (Ha) diterima. Ini berarti secara statistik, daya tahan kedua merk bola lampu tersebut berbeda

Merk "B" menunjukkan perbedaan yang signifikan dalam rata-rata daya tahan hidupnya. Sebagai contoh, dalam sampel kecil yang diambil, sebuah perusahaan produsen alat rumah tangga sedang melakukan uji hipotesis untuk membandingkan dua jenis produk mereka. Dalam percobaan yang dilakukan, diperoleh data sebagai berikut:

• 10 produk A memiliki rata-rata daya tahan hidup 2.600 jam, dengan deviasi standar 300 jam.
• 15 produk B memiliki rata-rata daya tahan hidup 2.400 jam, dengan deviasi standar 250 jam.

Berdasarkan hasil uji coba ini, dapatkah disimpulkan bahwa kualitas daya tahan hidup kedua produk tersebut berbeda? (Dengan asumsi: distribusi normal, variansi yang sama, dan tingkat signifikansi 0,05).

Kesimpulan:
Karena t = 1,81 < t(23; 0,025) = 2,069, maka Ho diterima dan Ha ditolak. Dengan demikian, dapat disimpulkan bahwa kualitas daya tahan hidup lampu A dan lampu B tidak menunjukkan perbedaan yang signifikan, atau dengan kata lain, keduanya memiliki daya tahan hidup yang sama