gunakan untuk ujian semester genap maupun ganjil, di perkuliahan Anda, silakan di copy.
Mata Kuliah : Analisis Real I Pengampu : __________
Kode : MAA 321 Hari/Tgl : __________
Prodi : Mat & Pend Mat (Kur 2002) Jam Ujian : _________
Semester : VIII Ruang : __________
Mata Kuliah : Analisis Real I Pengampu : __________
Kode : MAA 321 Hari/Tgl : __________
Prodi : Mat & Pend Mat (Kur 2002) Jam Ujian : _________
Semester : VIII Ruang : __________
1. Gunakan induksi
matematika untuk menunjukkan bahwa 2n< (n 1)! untuk n > 5.
2. Himpunan A ⊂ R dengan A ≠ ∅ dan A terbatas, serta himpunan bA dide nisikan sebagai bA = {ba : a ∈ ) dengan b < 0. Apakah inf (bA) = b inf A? Jika ya, buktikan! Jika tidak, maka seharusnya inf (bA) =
? Buktikan!
3. Tunjukkan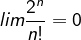
bahwa . [Hint: gunakan hasil dari soal no 1.]
4. Diketahui
dan a ≥ 0 apakah 
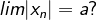Buktikan jawaban anda!
Bagaimana jika dan a < 0, apakah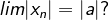 
2. Himpunan A ⊂ R dengan A ≠ ∅ dan A terbatas, serta himpunan bA dide nisikan sebagai bA = {ba : a ∈ ) dengan b < 0. Apakah inf (bA) = b inf A? Jika ya, buktikan! Jika tidak, maka seharusnya inf (bA) =
? Buktikan!
3. Tunjukkan
4. Diketahui
Bagaimana jika
Posting Komentar
Berkomentar sesuai dengan judul blog ini yah, berbagi ilmu, berbagi kebaikan, kunjungi juga otoriv tempat jual aksesoris motor dan mobil lengkap